
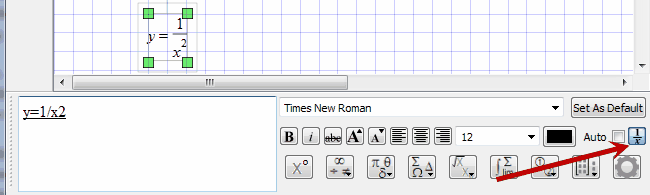
Then, we could write $f$ as a function with a single parameter (a function machine with a single dial): We could represent the base of the exponentiation by a parameter $b$. We could capture both functions using a single function machine but dials to represent parameters influencing how the machine works. The above exponential functions $f(x)$ and $g(x)$ are two different functions, but they differ only by the change in the base of the exponentiation from 2 to 1/2. The function machine metaphor is useful for introducing parameters into a function. Parameters of the exponential functionĪs with any function, the action of an exponential function $f(x)$ can be captured by the function machine metaphor that takes inputs $x$ and transforms them into the outputs $f(x)$. The presence of this doubling time or half-life is characteristic of exponential functions, indicating how fast they grow or decay. In the exponential decay of $g(x)$, the function shrinks in half every time you add one to its input $x$. In the exponential growth of $f(x)$, the function doubles every time you add one to its input $x$. It gets rapidly smaller as $x$ increases, as illustrated by its graph. For example, an exponential function arises in simple models of bacteria growthĪn exponential function can describe growth or decay. Exponential functions are solutions to the simplest types of dynamical systems. A simple example is the functionĪs illustrated in the above graph of $f$, the exponential function increases rapidly. To form an exponential function, we let the independent variable be the exponent. The exponential function is one of the most important functions in mathematics (though it would have to admit that the linear function ranks even higher in importance).


 0 kommentar(er)
0 kommentar(er)
